三 平方 の 定理 直角 三角形 130696

直角三角形において、「直角」をはさむ2つの辺の長さを \(a,b\)、斜辺の長さを \(c\) としたとき 三平方の定理（ピタゴラスの定理）と公式の証明忍者が用いた三角の知恵｜アタリマエ！3：4：5の三角形で，本当に直角ができるのでしょうか。 三角形の辺の長さの比と角の大きさには，どんな関係があるのでしょうか。 3：4：5は，斜辺の対角が直角です。このことは，三平方の定理として知られています。 3：4：5三平方の定理は、直角三角形に対して使えるものなんだけど 直角三角形がなければ、今回の問題のように補助線を引いて作っちゃえばOKだね！ ということで、三平方の定理を使って面積を求める方法についてでした！ 直角三角形がなければ、自分で作る！ これがすごく大切なポイントでした

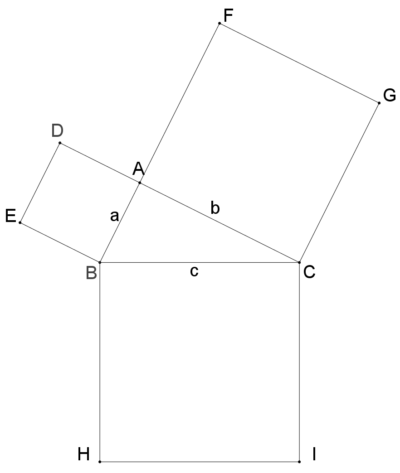
三平方の定理の証明 ユークリッドの証明 Fukusukeの数学めも

三 平方 の 定理 直角 三角形

三 平方 の 定理 直角 三角形-45°：45°：90°の直角三角形 こちらは直角以外の2角が2つとも45°になっている三角形、すなわち直角二等辺三角形です。これは辺の比が1：1：√2になります。 この三角形の角度と辺の比も必ず覚えておくようにしましょう。 三平方の定理の計算問題の解き方下の図のように補助線をひくと、\(2\) つの直角三角形に割れます。 まずは、左下のピンクの直角三角形に三平方の定理を用います。 \(y^2=2^29^2\) \(y^2=85\) この \(y^2\) の値は、右上の直角三角形に三平方の定理を用いたときに そのまま使えます。 \(y^2=x^25^2

三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 ベネッセコーポレーション

直角三角形の辺の比 を3つ紹介するよ。 比その1 「1 2 √3」 まず覚えておいておくべき直角三角形の辺の比は、 12√3 だよ。 この辺の比になる直角三角形の角度は、 30° 60° 90° になってるんだ。三角定規型 暗記しておくべき直角三角形があります。 それは三角定規の形です。 三角定規は \(2\) 種類あります。 その \(2\) 種類は必ず暗記すべき特別な直角三角形です。 45° 45° 90° まずはじめに直角二等辺三角形タイプです。 これは「正方形半分タイプ」という名前でも覚えておきましょう。だから、この三角形は直角三角形ではありません。 このように、三平方の定理の逆を用いると3辺の長さからその三角形が直角三角形になるかどうかを調べることができるというわけです。 便利ですね～♪ ここからは高校生になってから学習すると思いますが

三角定規型 暗記しておくべき直角三角形があります。 それは三角定規の形です。 三角定規は \(2\) 種類あります。 その \(2\) 種類は必ず暗記すべき特別な直角三角形です。 45° 45° 90° まずはじめに直角二等辺三角形タイプです。 これは「正方形半分タイプ」という名前でも覚えておきましょう。三平方の定理の公式を紹介します。下の図のように直角三角形の直角を挟む2辺をa,bとし、斜辺をcとすると a²b²=c² の等式が成立することを三平方の定理と言います。 三平方の定理の証明 三平方の定理の証明について紹介したいと思います。直角三角形三边长度符合勾股定理，其中一个直角边长度的平方 加上另一个直角边长度的平方等于斜边长度的平方。三十度所对的直角边等于斜边的一半。直角三角形斜边上的中线等于斜边的一半 本回答被网友采纳 已赞过 已踩过 你对这个回答的评价是？ 评论 收起 网际超人 1428 · ta获得

方の定理を利用するた めの直角三角形を見い だすことができる ・平面図形のなかに，三 平方の定理を利用する ための直角三角形を見 いだすことができる． ・空間図形のなかに，三 平方の定理を利用する ための直角三角形を見 いだすことができる．三平方の定理は、 直角三角形の三辺をa,b,cとする。斜辺(最も長い辺)をcとすると、 c² = a² b² が成り立つ というものです。別名ピタゴラスの定理とも呼ばれます。 式は綺麗ですが、二乗が出てきます。なので、実際にこの定理で辺の長さを計算すると、平方根を求める作業が必要になりじつは、三平方の定理（ピタゴラスの定理）のすごいところは、 直角三角形の2辺の長さがわかれば、残りの辺の長さがわかる ってところなんだ。 たとえば、斜辺の長さ13cm、その他一辺の長さが5cmの直角三角形DEFがあったとしよう。

三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト

特別な直角三角形の辺の比 無料で使える中学学習プリント

三平方の定理の公式を紹介します。下の図のように直角三角形の直角を挟む2辺をa,bとし、斜辺をcとすると a²b²=c² の等式が成立することを三平方の定理と言います。 三平方の定理の証明 三平方の定理の証明について紹介したいと思います。45°：45°：90°の直角三角形 こちらは直角以外の2角が2つとも45°になっている三角形、すなわち直角二等辺三角形です。これは辺の比が1：1：√2になります。 この三角形の角度と辺の比も必ず覚えておくようにしましょう。 三平方の定理の計算問題の解き方三角定規型 暗記しておくべき直角三角形があります。 それは三角定規の形です。 三角定規は \(2\) 種類あります。 その \(2\) 種類は必ず暗記すべき特別な直角三角形です。 45° 45° 90° まずはじめに直角二等辺三角形タイプです。 これは「正方形半分タイプ」という名前でも覚えておきましょう。

三平方の定理 無料で使える中学学習プリント

三平方の定理 覚えておきたい基本公式を解説 数スタ

直角三角形の辺の比 を3つ紹介するよ。 比その1 「1 2 √3」 まず覚えておいておくべき直角三角形の辺の比は、 12√3 だよ。 この辺の比になる直角三角形の角度は、 30° 60° 90° になってるんだ。ピタゴラスの定理（ピタゴラスのていり）は、直角三角形の3辺の長さの関係を表す等式である。三平方の定理（さんへいほうのていり）、勾股弦の定理（こうこげんのていり）とも呼ばれる。1 1 概要 2 ピタゴラス数 21 ピタゴラス数の性質 22 Jesmanowicz 予想 3 一般化 31 角の一般化 32 指数の三平方の定理をもっと使いこなしていくために、下の \(\bf{4}\) パターンの直角三角形の角度と辺の比を覚えましょう。 これらの形を暗記すると、よりスピーディに計算できるようになります。

知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より

数学 中3 61 三平方の定理 基本編 Youtube

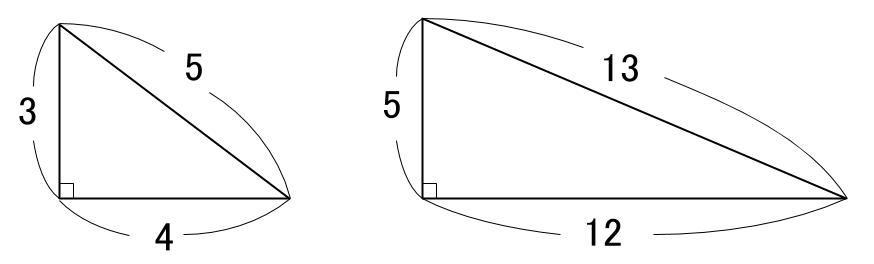
三平方の定理は直角三角形の直角を挟む二辺の関係を示しています。 c 2 の平方 根を見つけ 与えられた三角形を見ます。この時点で三つ全ての角の角度と辺aの長さが分かっています。そこで、これらの情報を正弦定理に代入して、残り二辺の長さを三平方の定理をもっと使いこなしていくために、下の \(\bf{4}\) パターンの直角三角形の角度と辺の比を覚えましょう。 これらの形を暗記すると、よりスピーディに計算できるようになります。知ってて損はない 直角三角形 中学受験ですので、三辺の 辺の比が整数となる直角三角形 がよく出題されます。 左側の $\textcolor{red}{345}$ の 三角形 は 超頻出 なので、覚えておいて欲しいですが、他の2つは そんなのもあるんだぁ~ 程度で良いかなぁ と

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

三平方の定理 おやじさん ネット

まとめ：三平方の定理（ピタゴラスの定理）を使えば直角三角形の辺の長さは大体わかる！ 三平方の定理で、直角三角形の辺の長さを求める問題はどうだった？ 今日勉強した問題のパターンは4つだったな？ 超基本タイプ;

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

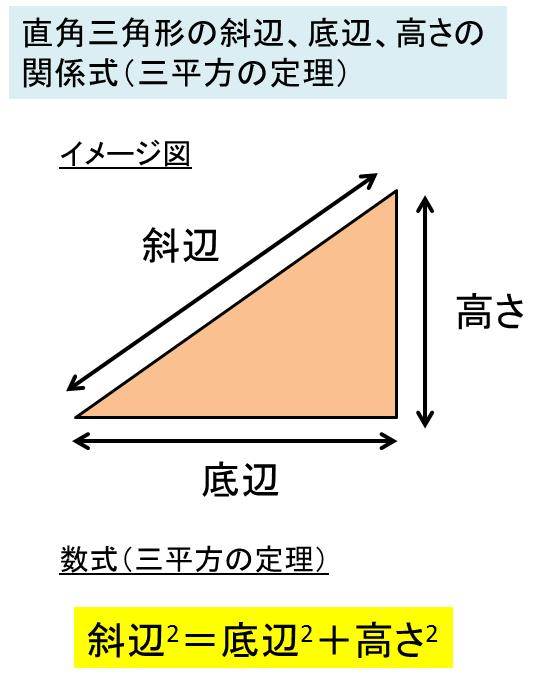
Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方

三平方の定理 ピタゴラスの定理

中学数学 三平方の定理の利用

Mathematics 三平方の定理 ２ 特別な直角三角形 働きアリ

三平方の定理 覚えること 三角定規 苦手な数学を簡単に

三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく

三平方の定理の証明と使い方

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

中3数学 三平方の定理5 特別な直角三角形の辺の比 すべて無料 星組の中学数学講座

無料 中３数学 基本解説 解答プリント 334 三平方の定理２ 比の利用

余弦定理と三平方の定理 Cinderellajapan

直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

三平方の定理の証明です 線を引いている部分がどういう事なのか分かりません Clear

三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ１０選 遊ぶ数学

直角三角形の辺の長さ 合同条件 面積について アタリマエ

三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題

三平方の定理について考える４ 三角形の相似を使った証明方法 身勝手な主張

三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ

三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト

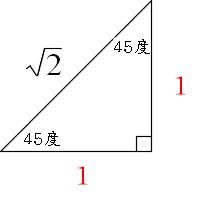
Mathematics 三平方の定理 ２ 特別な直角三角形 働きアリ

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4

三平方の定理の応用

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

三平方の定理の４通りの美しい証明 高校数学の美しい物語

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

三平方の定理 やややさしい数学

三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 ベネッセコーポレーション

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理 スタディーx

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

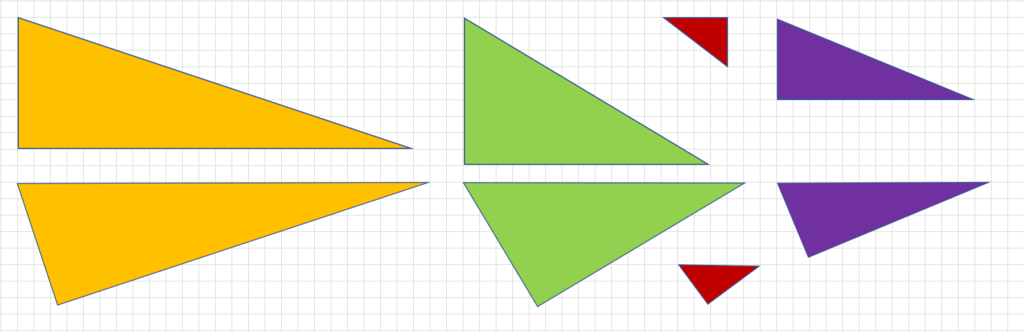
中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

三平方の定理を直角三角形二つで証明 Youtube

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

三平方の定理の証明と使い方

高校入試 英語 数学 三平方の定理の逆

三平方の定理の証明 直感的に分かる図で解説します 数学fun

三平方の定理の証明 相似を利用した証明１ Fukusukeの数学めも

三平方の定理の２つの証明方法 理数系無料オンライン学習 Kori

交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー

三平方の定理 自動計算サイト

三平方の定理の証明 正方形の面積を使う方法 数学教材

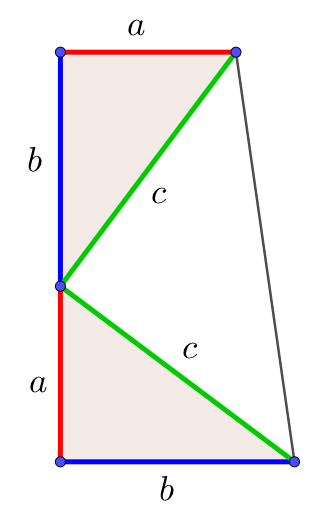
三平方の定理の証明３ 大統領の台形 キソカラ

三平方の定理とは 証明方法や例題についても解説 スタモ 受験 入試 学習の総合サイト

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

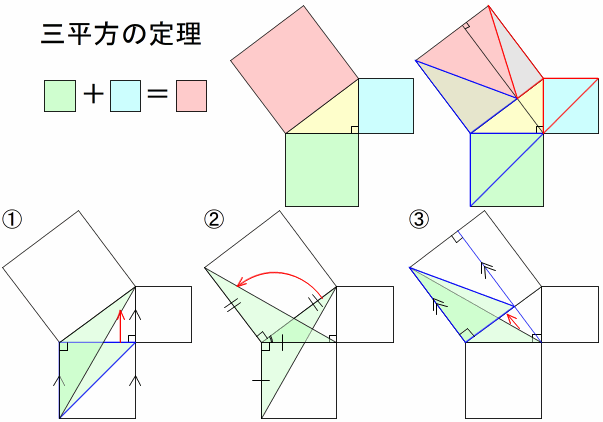
３ ４ ５の三角形で 本当に直角ができる Note Board

三平方の定理

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

三平方の定理の証明 相似な三角形を使う方法 数学教材

三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

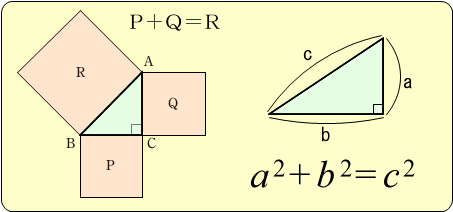
見えますか タイルの模様からピタゴラスの定理 Note Board

三平方の定理の証明と使い方

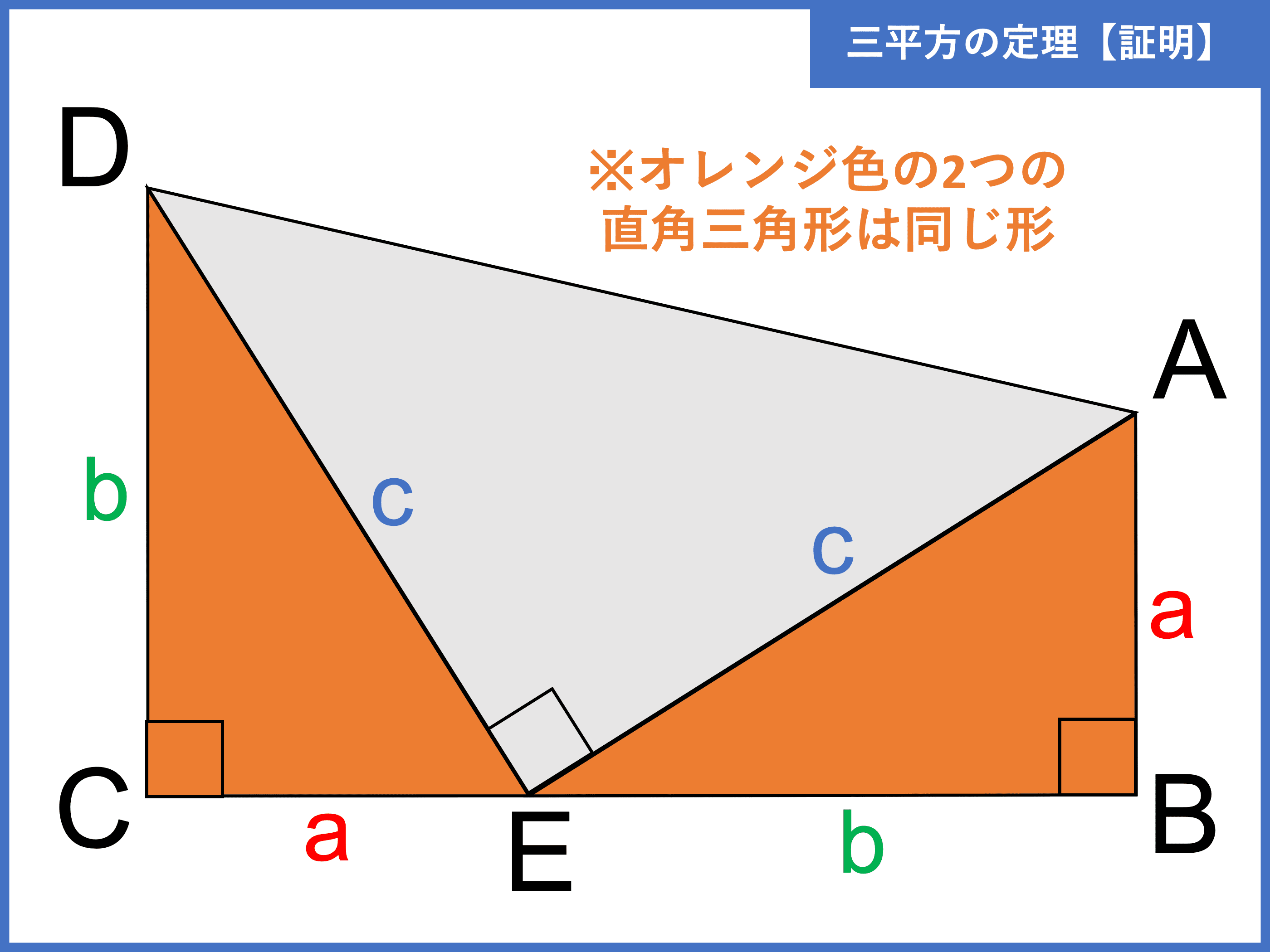
三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

三平方の定理

三平方の定理で辺を求める Youtube

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

鋭角 鈍角三角形 三平方の定理を使って見分ける方法を解説 数スタ

中学数学 三平方の定理 30 60 90 の直角三角形 オンライン無料塾 ターンナップ

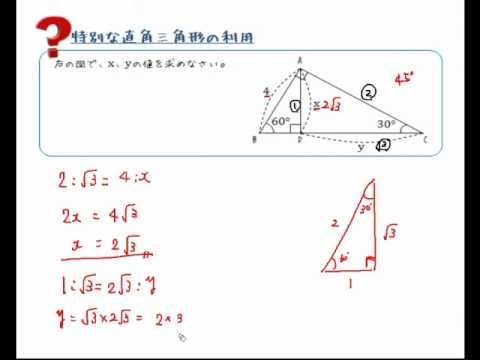
特別な直角三角形の利用 Youtube

三平方の定理の証明 ユークリッドの証明 Fukusukeの数学めも

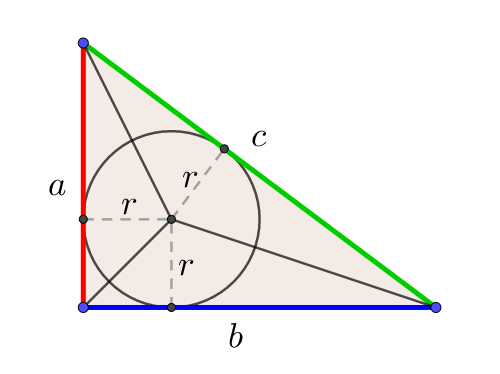
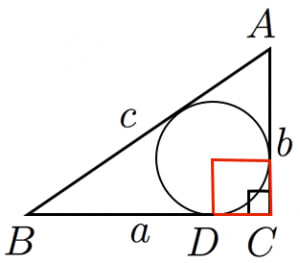
三平方の定理の証明４ 直角三角形と内接円 キソカラ

三平方の定理 特別な直角三角形 イ弋マ本ゼミナール

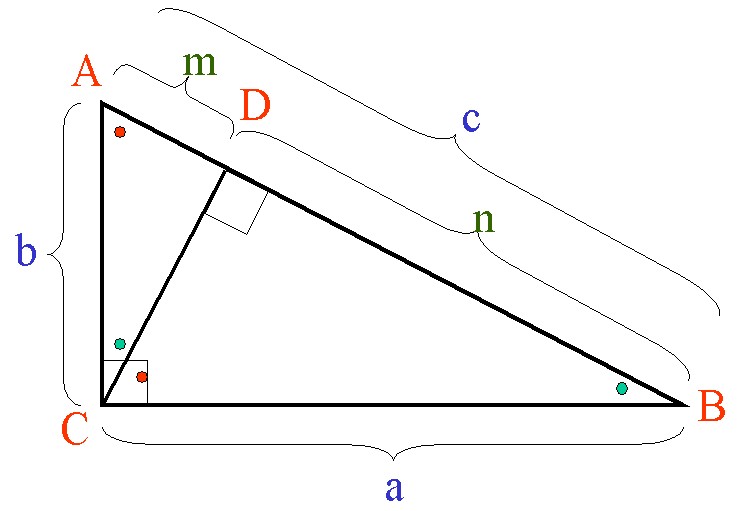
三平方の定理 花鳥風月の風流を楽しんでる暇もない

中学数学 三平方の定理の利用

三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ

余弦定理と三平方の定理 Cinderellajapan

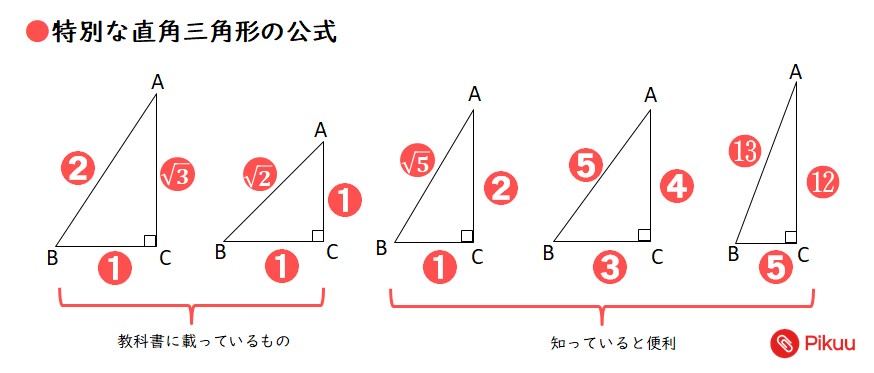
高校入試対策数学 特別な直角三角形を使った問題 Pikuu

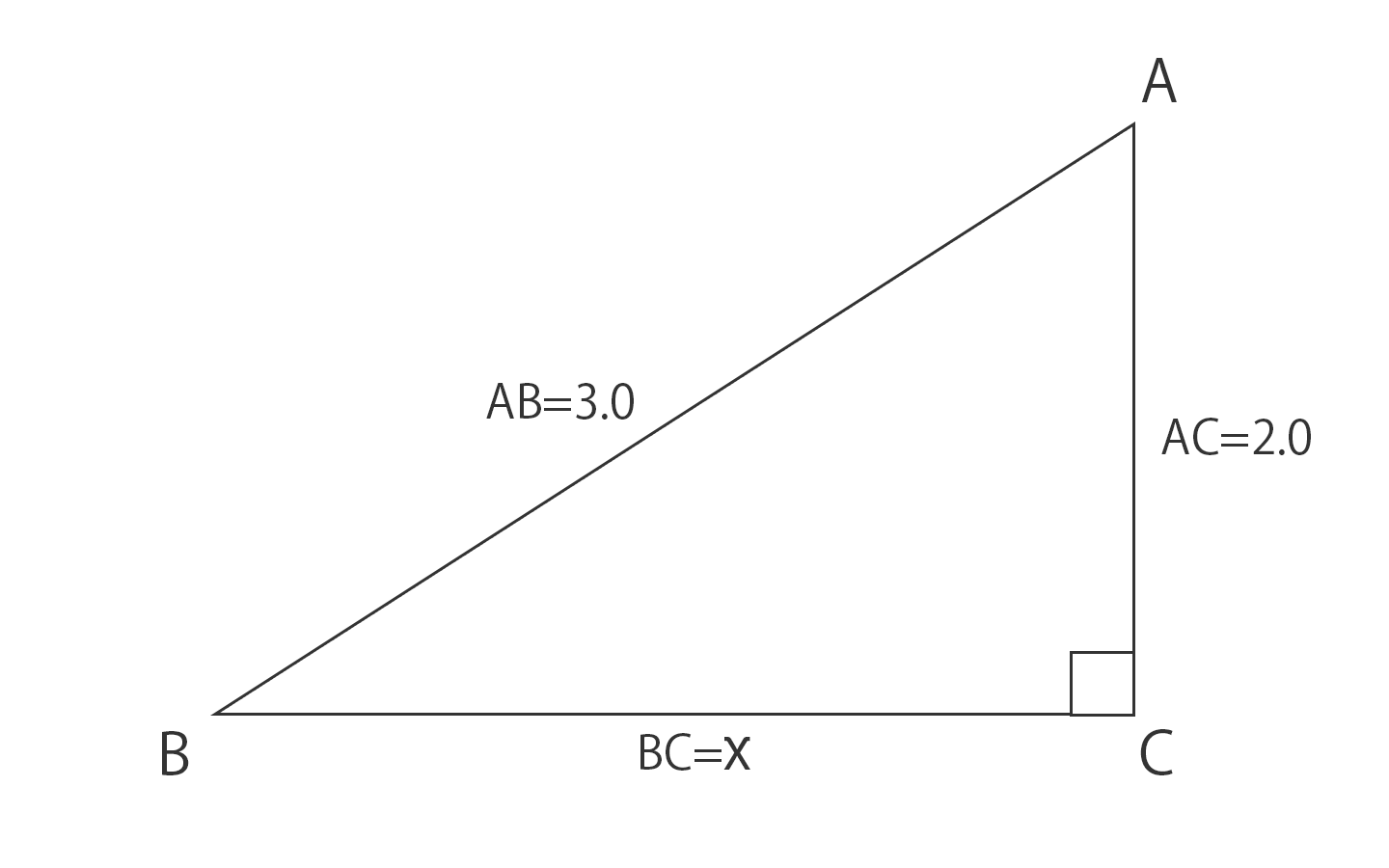
Python 三平方の定理 Unpyside

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

中学数学 三平方の定理 三平方の定理とは オンライン無料塾 ターンナップ

中学数学 三平方の定理

30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学

勉強しよう数学0 やさしいピタゴラスの定理 三平方の定理 の証明

三平方の定理

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

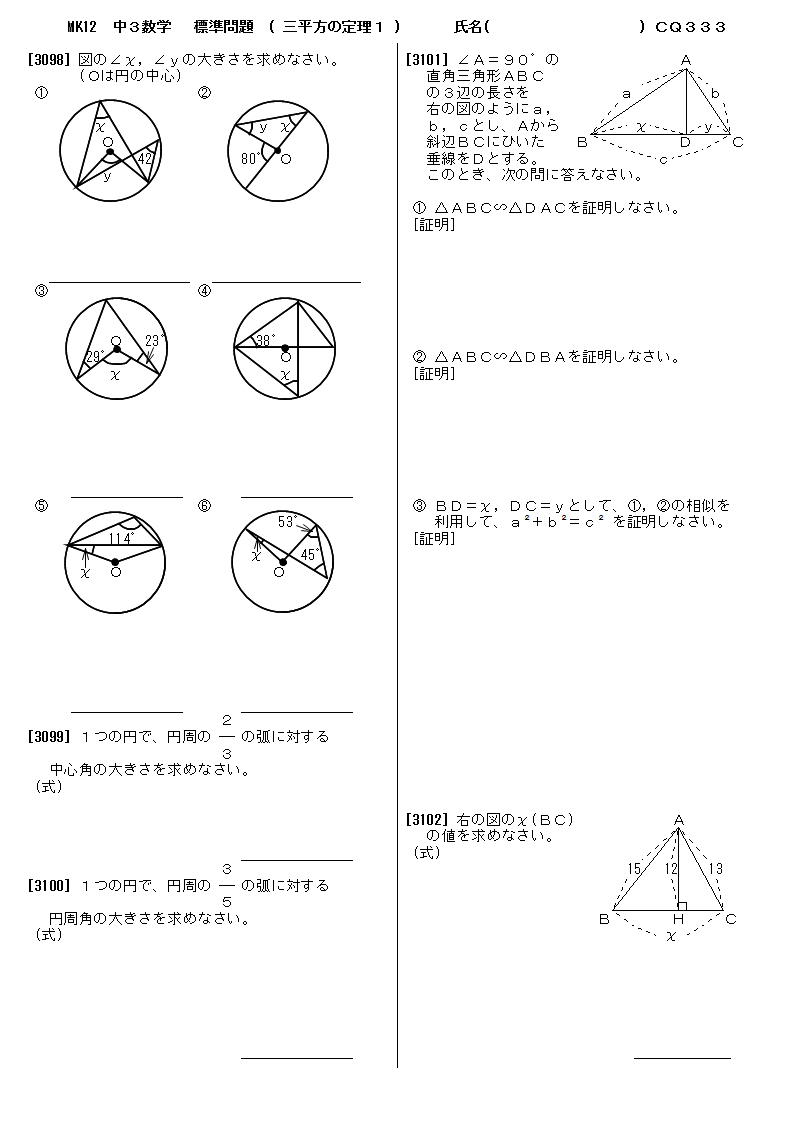
無料 中３数学 標準問題 問題プリント 333 三平方の定理１ 直角三角形

数学切り抜き帳